describe what is happening in the hydrogen discharge tube for these line spectra to be produced.
| THE ATOMIC HYDROGEN EMISSION SPECTRUM This page introduces the atomic hydrogen emission spectrum, showing how it arises from electron movements between energy levels within the atom. It too looks at how the spectrum tin exist used to find the ionisation free energy of hydrogen. What is an emission spectrum? Observing hydrogen's emission spectrum A hydrogen discharge tube is a slim tube containing hydrogen gas at low pressure with an electrode at each end. If you put a loftier voltage across this (say, 5000 volts), the tube lights up with a brilliant pinkish glow. If the low-cal is passed through a prism or diffraction grating, it is split into its various colours. What yous would encounter is a small-scale role of the hydrogen emission spectrum. Most of the spectrum is invisible to the heart considering it is either in the infra-red or the ultra-violet. The photograph shows function of a hydrogen discharge tube on the left, and the 3 most easily seen lines in the visible part of the spectrum on the correct. (Ignore the "smearing" - particularly to the left of the cherry line. This is caused by flaws in the way the photograph was taken. Run into note below.) | |
| Note:This photo is past courtesy of Dr Rod Nave of the Department of Physics and Astronomy at Georgia State University, Atlanta. The photograph comes from notes most the hydrogen spectrum in his HyperPhysics pages on the Academy site. If you are interested in more an introductory look at the subject area, that is a expert place to become. Ideally the photo would show three make clean spectral lines - night blueish, cyan and red. The red smearing which appears to the left of the red line, and other similar smearing (much more than difficult to see) to the left of the other 2 lines probably comes, according to Dr Nave, from stray reflections in the set-upward, or perhaps from flaws in the diffraction grating. I have chosen to apply this photograph anyway because a) I think information technology is a stunning image, and b) it is the merely one I have ever come across which includes a hydrogen discharge tube and its spectrum in the same image. | |
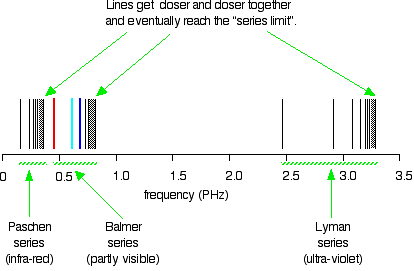
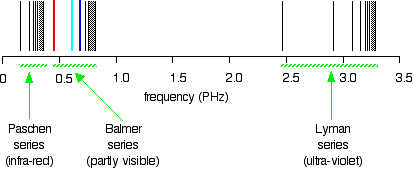
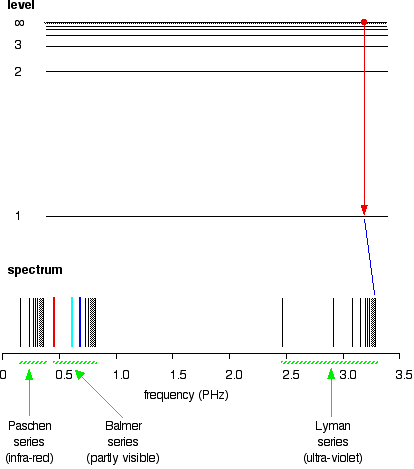
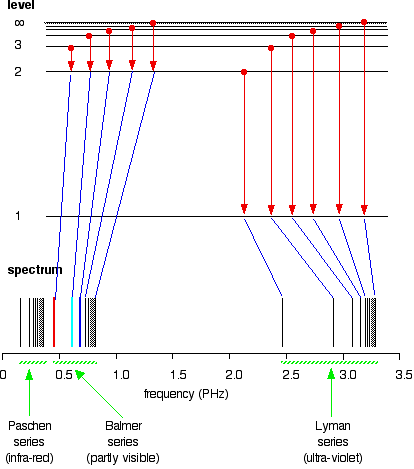
| Extending hydrogen'south emission spectrum into the UV and IR There is a lot more than to the hydrogen spectrum than the three lines you tin can see with the naked eye. It is possible to detect patterns of lines in both the ultra-violet and infra-red regions of the spectrum as well. These fall into a number of "serial" of lines named later on the person who discovered them. The diagram beneath shows three of these series, simply there are others in the infra-red to the left of the Paschen series shown in the diagram. The diagram is quite complicated, so we volition look at it a flake at a time. Look get-go at the Lyman series on the right of the diagram - this is the most spread out one and easiest to run into what is happening. | |
| Annotation:The frequency scale is marked in PHz - that's petaHertz. Yous are familiar with prefixes like kilo (meaning a m or ten3 times), and mega (significant a million or 106 times). Peta means 10fifteen times. And so a value like 3 PHz means three x 1015 Hz. If you are worried near "Hertz", it simply means "cycles per 2nd". | |
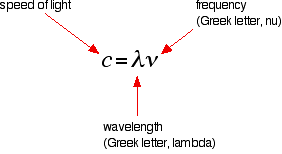
| The Lyman series is a serial of lines in the ultra-violet. Notice that the lines get closer and closer together as the frequency increases. Eventually, they get so close together that it becomes incommunicable to meet them as anything other than a continuous spectrum. That's what the shaded bit on the correct-hand end of the series suggests. Then at one detail point, known as the series limit , the series stops. If you at present await at the Balmer series or the Paschen series, yous volition run into that the pattern is just the aforementioned, simply the series have get more compact. In the Balmer series, find the position of the iii visible lines from the photograph further upwardly the page. Complicating everything - frequency and wavelength You volition often observe the hydrogen spectrum drawn using wavelengths of light rather than frequencies. Unfortunately, because of the mathematical relationship between the frequency of light and its wavelength, you become two completely different views of the spectrum if you plot it against frequency or confronting wavelength. The relationship between frequency and wavelength The mathematical relationship is: Rearranging this gives equations for either wavelength or frequency. What this means is that there is an changed human relationship betwixt the two - a loftier frequency means a low wavelength and vice versa. | |
| Note:Y'all will sometimes detect frequency given the much more than obvious symbol, f. | |
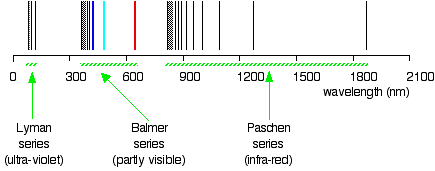
| Drawing the hydrogen spectrum in terms of wavelength This is what the spectrum looks similar if you plot it in terms of wavelength instead of frequency: . . . and just to remind you what the spectrum in terms of frequency looks like: Is this disruptive? Well, I find it extremely disruptive! So what do you lot do well-nigh it? For the residue of this page I shall but look at the spectrum plotted against frequency, considering it is much easier to relate information technology to what is happening in the atom. Be enlightened that the spectrum looks different depending on how it is plotted, simply, other than that, ignore the wavelength version unless information technology is obvious that your examiners desire it. If you attempt to larn both versions, y'all are only going to go them muddled up! | |
| Notation:Syllabuses probably won't be very helpful about this. You need to look at past papers and mark schemes. If you lot are working towards a Great britain-based test and don't have these things, you can find out how to get hold of them by going to the syllabuses folio. | |
| Explaining hydrogen's emission spectrum The Balmer and Rydberg Equations By an astonishing bit of mathematical insight, in 1885 Balmer came upwards with a simple formula for predicting the wavelength of any of the lines in what we now know every bit the Balmer series. Three years later, Rydberg generalised this so that information technology was possible to work out the wavelengths of whatsoever of the lines in the hydrogen emission spectrum. What Rydberg came upwardly with was: RH is a constant known every bit the Rydberg constant . n1 and north2 are integers (whole numbers). n2 has to be greater than north1. In other words, if none is, say, ii then nii tin can be any whole number between 3 and infinity. The diverse combinations of numbers that yous can slot into this formula allow you summate the wavelength of whatever of the lines in the hydrogen emission spectrum - and there is shut understanding between the wavelengths that you lot get using this formula and those found past analysing a existent spectrum. | |
| Note:If you run across a version of Balmer'southward original equation, information technology won't expect similar this. In Balmer's equation, due north1 is ever 2 - considering that gives the wavelengths of the lines in the visible part of the spectrum which is what he was interested in. His original equation was likewise organised differently. The modern version shows more clearly what is going on. | |
| You can besides use a modified version of the Rydberg equation to summate the frequency of each of the lines. Y'all tin can work out this version from the previous equation and the formula relating wavelength and frequency further upwards the page. | |
| Notation:You lot may come beyond versions of the Rydberg equation where the n1 and due northtwo are the other way around, or they may even be swapped for letters like m and due north. Whichever version you lot use, the bigger number must always be the one at the bottom of the correct-hand term - the one you take away. If you lot get them the wrong style around, it is immediately obvious if you lot outset to do a adding, because you volition finish upwardly with a negative respond! | |
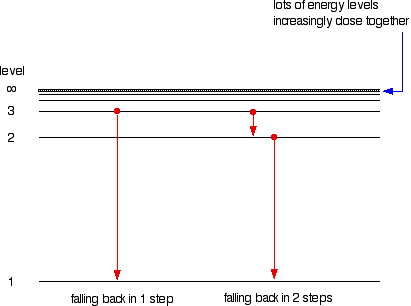
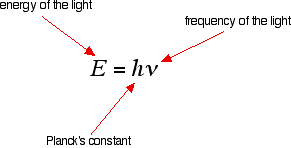
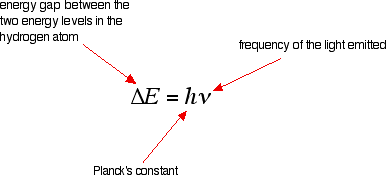
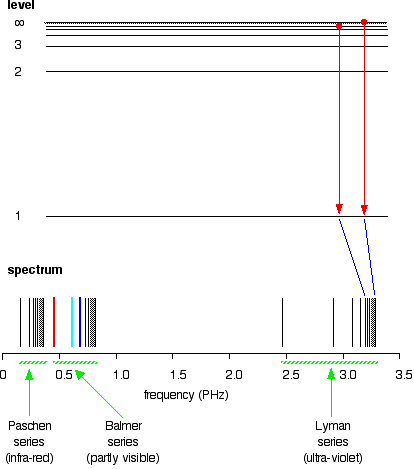
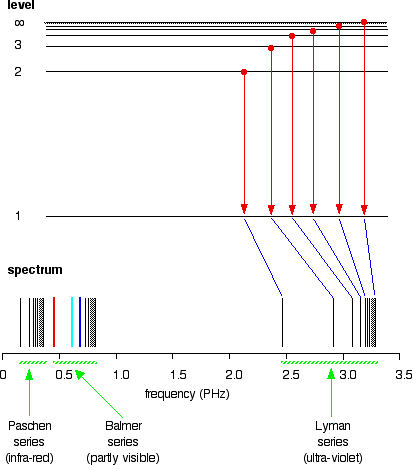
| The origin of the hydrogen emission spectrum The lines in the hydrogen emission spectrum class regular patterns and can be represented by a (relatively) uncomplicated equation. Each line tin be calculated from a combination of uncomplicated whole numbers. Why does hydrogen emit light when information technology is excited past existence exposed to a high voltage and what is the significance of those whole numbers? When cypher is heady it, hydrogen'southward electron is in the first energy level - the level closest to the nucleus. But if you supply energy to the cantlet, the electron gets excited into a higher energy level - or even removed from the atom birthday. The high voltage in a belch tube provides that energy. Hydrogen molecules are first broken up into hydrogen atoms (hence the atomic hydrogen emission spectrum) and electrons are and then promoted into higher energy levels. Suppose a particular electron was excited into the third energy level. This would tend to lose free energy again past falling back downwards to a lower level. Information technology could do this in two different means. It could fall all the style back down to the starting time level again, or it could fall back to the second level - and and so, in a 2d jump, down to the offset level. Tying particular electron jumps to individual lines in the spectrum If an electron falls from the 3-level to the 2-level, information technology has to lose an corporeality of free energy exactly the same equally the energy gap betwixt those two levels. That free energy which the electron loses comes out as calorie-free (where "light" includes UV and IR likewise as visible). Each frequency of light is associated with a particular energy by the equation: The college the frequency, the higher the energy of the light. If an electron falls from the 3-level to the 2-level, red light is seen. This is the origin of the ruby-red line in the hydrogen spectrum. Past measuring the frequency of the red light, you tin can work out its energy. That free energy must be exactly the same equally the energy gap betwixt the 3-level and the 2-level in the hydrogen atom. The last equation can therefore be re-written as a measure of the energy gap between two electron levels. The greatest possible autumn in energy volition therefore produce the highest frequency line in the spectrum. The greatest fall will be from the infinity level to the 1-level. (The significance of the infinity level will be made clear later.) The side by side few diagrams are in two parts - with the energy levels at the summit and the spectrum at the bottom. If an electron fell from the 6-level, the fall is a little fleck less, and and then the frequency will exist a little bit lower. (Because of the scale of the diagram, information technology is impossible to draw in all the jumps involving all the levels between 7 and infinity!) . . . and as y'all piece of work your style through the other possible jumps to the 1-level, you have deemed for the whole of the Lyman series. The spacings between the lines in the spectrum reflect the manner the spacings between the free energy levels change. If you practise the aforementioned thing for jumps downward to the two-level, y'all end up with the lines in the Balmer series. These energy gaps are all much smaller than in the Lyman series, and and then the frequencies produced are also much lower. The Paschen serial would be produced by jumps down to the iii-level, but the diagram is going to get very messy if I include those likewise - not to mention all the other series with jumps down to the iv-level, the v-level and so on. The significance of the numbers in the Rydberg equation n1 and n2 in the Rydberg equation are just the energy levels at either end of the jump producing a particular line in the spectrum. For example, in the Lyman serial, n1 is ever 1. Electrons are falling to the 1-level to produce lines in the Lyman series. For the Balmer serial, nane is always ii, because electrons are falling to the 2-level. n2 is the level being jumped from. We have already mentioned that the red line is produced by electrons falling from the three-level to the 2-level. In this case, and then, n2 is equal to 3. The significance of the infinity level The infinity level represents the highest possible free energy an electron can have as a function of a hydrogen atom. So what happens if the electron exceeds that energy by fifty-fifty the tiniest bit? The electron is no longer a office of the atom. The infinity level represents the point at which ionisation of the atom occurs to class a positively charged ion. Using the spectrum to find hydrogen's ionisation energy When there is no boosted energy supplied to it, hydrogen's electron is found at the 1-level. This is known as its ground country. If you supply enough energy to move the electron up to the infinity level, you have ionised the hydrogen. The ionisation free energy per electron is therefore a mensurate of the distance between the 1-level and the infinity level. If you look back at the last few diagrams, you will discover that that particular energy bound produces the series limit of the Lyman series. | |
| Note:Up to at present nosotros have been talking about the energy released when an electron falls from a higher to a lower level. Evidently if a certain amount of energy is released when an electron falls from the infinity level to the 1-level, that same amount will exist needed to button the electron from the one-level up to the infinity level. | |
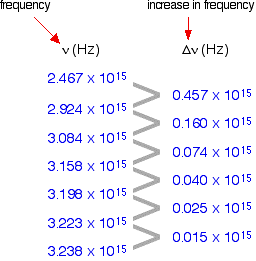
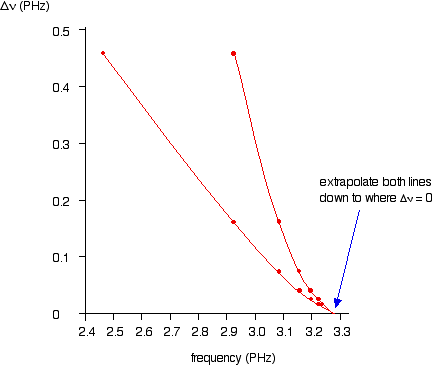
| If yous can determine the frequency of the Lyman series limit, you tin can employ it to calculate the free energy needed to move the electron in 1 atom from the 1-level to the point of ionisation. From that, you can calculate the ionisation energy per mole of atoms. The problem is that the frequency of a series limit is quite difficult to discover accurately from a spectrum because the lines are then shut together in that region that the spectrum looks continuous. Finding the frequency of the series limit graphically Here is a listing of the frequencies of the seven almost widely spaced lines in the Lyman series, together with the increase in frequency as you go from one to the next. Equally the lines go closer together, evidently the increment in frequency gets less. At the series limit, the gap between the lines would be literally goose egg. That means that if you were to plot the increases in frequency against the actual frequency, you could extrapolate (proceed) the curve to the point at which the increase becomes zilch. That would be the frequency of the serial limit. In fact you lot can actually plot two graphs from the data in the table above. The frequency departure is related to two frequencies. For instance, the figure of 0.457 is found by taking 2.467 away from 2.924. So which of these two values should you plot the 0.457 against? It doesn't thing, as long as you lot are always consistent - in other words, as long as you e'er plot the difference against either the college or the lower effigy. At the indicate you are interested in (where the difference becomes nothing), the two frequency numbers are the same. As you will see from the graph below, by plotting both of the possible curves on the same graph, information technology makes it easier to decide exactly how to extrapolate the curves. Considering these are curves, they are much more than difficult to extrapolate than if they were directly lines. Both lines point to a series limit at about three.28 x tenxv Hz. | |
| Note:Remember that iii.28 PHz is the same as 3.28 x 1015 Hz. You can use the Rydberg equation to calculate the series limit of the Lyman series as a bank check on this figure: due north1 = ane for the Lyman series, and n2 = infinity for the series limit. one/(infinity)ii = zero. That gives a value for the frequency of 3.29 x 10fifteen Hz - in other words the ii values concord to within 0.iii%. | |
| So . . . now we tin calculate the energy needed to remove a single electron from a hydrogen cantlet. Remember the equation from higher up the page: Nosotros can work out the energy gap between the footing land and the point at which the electron leaves the atom past substituting the value we've got for frequency and looking upwards the value of Planck's constant from a information book. That gives you the ionisation energy for a unmarried atom. To observe the normally quoted ionisation energy, nosotros need to multiply this by the number of atoms in a mole of hydrogen atoms (the Avogadro constant) and and then carve up past 1000 to convert it into kilojoules. | |
| Note:It would be wrong to quote this to more than than 3 significant figures. The value for the frequency obtained from the graph is only to that accuracy. | |
| This compares well with the ordinarily quoted value for hydrogen's ionisation energy of 1312 kJ mol-1.
© Jim Clark 2006 (final modified August 2012) | |
Source: https://www.chemguide.co.uk/atoms/properties/hspectrum.html

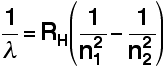
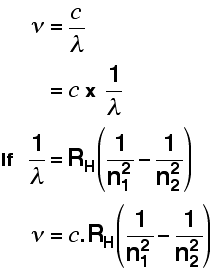
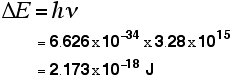
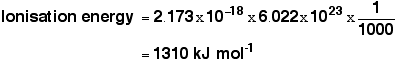
0 Response to "describe what is happening in the hydrogen discharge tube for these line spectra to be produced."
Post a Comment